数千年以来,我们涉及的和研究的主要是欧氏几何。欧氏几何主要是基于中小尺度上,点线、面之间的关系,这种观念与特定时期人类的实践认识水平是相适应的,有什么样的认识水平就有什么样的几何学。当人们全神贯注于机械运动时,头脑中的图象多是一些圆锥曲线、线段组合,受认识主客体的限制,欧氏几何具有很强的“人为”特征。
这样说并非要否定欧氏几何的辉煌历史,只是我们应当认识到欧氏几何是人们认识、把握客观世界的一种工具、但不是唯一的工具。
进入20世纪以后,科学的发展极为迅速。特别是二战以后,大量的新理论、新技术以及新的研究领域不断涌现,同以往相比,人们对物质世界以及人类社会的看法有了很大的不同。其结果是,有些研究对象已经很难用欧氏几何来描述了,如对植物形态的描述,对晶体裂痕的研究,等等。
美国数学家B,Mandelbrot曾出这样一个著名的问题:英格兰的海岸线到底有多长?这个问题在数学上可以理解为:用折线段拟合任意不规则的连续曲线是否一定有效?这个问题的提出实际上是对以欧氏几何为核心的传统几何的挑战。
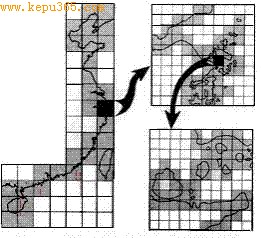
实际上,数学家们很早就认识到,有的曲线不能用欧式几何与微积分研究其长度。但那时解决办法是讨论具备什么条件的曲线有长度。而没有长度的曲线就没有深入研究。
此外,在湍流的研究。自然画面的描述等方面,人们发现传统几何依然是无能为力的。因此就产生一种新的能够更好地描述自然图形的几何学,就是分形几何。
下面是Kohn(克赫)曲线。

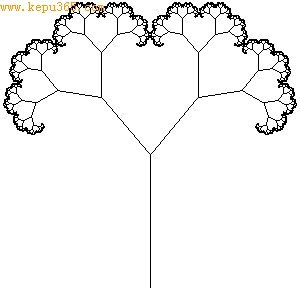
谢宾斯奇(W.Sierpinski,1882-1969)构造了谢氏曲线、地毯、海绵。

皮亚诺(peano)曲线

1975年,Mandelbrot在其《自然界中的分形几何》一书中引入了分形(fractal)这一概念。从字面意义上讲,fractal是碎块、碎片的意思,然而这并不能概括Mandelbrot的分形概念,尽管目前还没有一个让各方都满意的分形定义,但在数学上大家都认为分形有以下凡个特点:
(1)具有无限精细的结构;
(2)比例自相似性;
(3)一般它的分数维大子它的拓扑维数;
(4)可以由非常简单的方法定义,并由递归、迭代产生。
据说,南非海岸线的维数是1.02,英国西岸的维数是1.25。
分形无处不在。
分形几何学已在自然界与物理学中得到了应用。如在显微镜下观察落入溶液中的一粒花粉,会看见它不间断地作无规则运动(布朗运动),这是花粉在大量液体
[1] [2] 下一页
